Entre las medidas de tendencia central más utilizadas están la media aritmética, la mediana y la moda. Estos números dicen ciertas cualidades sobre los datos recogidos en determinado experimento.
Media aritmética para datos agrupados
La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos.
 es el símbolo de la media aritmética.
es el símbolo de la media aritmética.
 es el símbolo de la media aritmética.
es el símbolo de la media aritmética.Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la media es:


Mediana para datos agrupados
La mediana se encuentra en el intervalo donde la frecuencia acumulada llega hasta la mitad de la suma de las frecuencias absolutas.
Es decir tenemos que buscar el intervalo en el que se encuentre N/2
Li es el límite inferior de la clase donde se encuentra la mediana.
N/2 es la semisuma de las frecuencias absolutas.
Fi-1 (fa-1)es la frecuencia acumulada anterior a la clase mediana.
ai (A) es la amplitud de la clase.
La mediana es independiente de las amplitudes de los intervalos.
Moda para datos agrupados
La moda es el valor que tiene mayor frecuencia absoluta.
Se representa por Mo.
Se puede hallar la moda para variables cualitativas y cuantitativas.
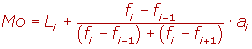
Li es el límite inferior de la clase modal.
fi es la frecuencia absoluta de la clase modal.
fi--1 es la frecuencia absoluta inmediatamente inferior a la en clase modal.
fi-+1 es la frecuencia absoluta inmediatamente posterior a la clase modal.
ai es la amplitud de la clase.
También se utiliza otra fórmula de la moda que da un valor aproximado de ésta:
Aprende a calcular las medidas de tendencia central con datos agrupados con los siguientes videos.
Actividad grado décimo para martes 5 de noviembre de 2019
Esta actividad hace parte de las actividades previas al plan de mejoramiento final.
Esta actividad hace parte de las actividades previas al plan de mejoramiento final.
Desarrollar en hojas de examen realizando todas las operaciones el siguiente problema.
Los siguientes datos representan los puntajes obtenidos en las pruebas icfes de los estudiantes de grado 11 en el 2018.
- Realizar la tabla de frecuencia de datos agrupados en 9 intervalos de amplitud 10, siendo el primer intervalo [10-20).
- Calcular las medidas de tendencia central (Media,Mediana y moda) de la tabla.
- Realizar una gráfica de barras de los datos luego de organizarlos en la tabla.
Al terminar lo anterior responde las siguientes preguntas y saca una conclusion de la tabla.
- ¿Cuántos estudiantes lograron sacar un puntaje en las icfes entre 30 y 45 puntos?
- ¿Cuántos estudiantes lograron sacar un puntaje en las icfes entre 40 y 100 puntos?
- ¿Cuántos estudiantes lograron sacar en las icfes menos de 60 puntos?
- ¿Qué porcentaje de estudiantes lograron sacar un puntaje en las icfes entre 30 y 49 puntos?
- ¿Qué porcentaje de estudiantes lograron sacar un puntaje en las icfes entre 50 y 59 puntos?
NOTA: Esta Actividad es solo para los estudiantes que no realizaron la actividad anterior.
- Recuerde que si sele da el el numero de intervalos y la amplitud no hay necesidad de buscarla.
- Si tiene alguna duda referente a la actividad puede dejarla en los comentarios, la responderé lo mas pronto posible.
- Comparte él link con tus compañeros para que todos puedan realizar la actividad.
Fuentes:
- Bellhouse, D. R. (2011). Abraham De Moivre: Setting the Stage for Classical Probability and Its Applications. CRC Press.
- Cifuentes, J. F. (2002). Introduccion a la Teoria de Probabilidad. Univ. Nacional de Colombia.
- Daston, L. (1995). Classical Probability in the Enlightenment. Princeton University Press.
- Larson, H. J. (1978). Introducción a la teoría de probabilidades e inferencia estadística. Editorial Limusa.
- Martel, P. J., & Vegas, F. J. (1996). Probabilidad y estadística matemática: aplicaciones en la práctica clínica y en la gestión sanitaria. Ediciones Díaz de Santos.
- Vázquez, A. L., & Ortiz, F. J. (2005). Métodos estadísticos para medir, describir y controlar la variabilidad. Ed. Universidad de Cantabria.
- Vázquez, S. G. (2009). Manual de Matemáticas para acceso a la Universidad. Editorial Centro de Estudios Ramon Areces SA.

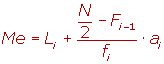
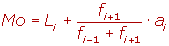

No hay comentarios:
Publicar un comentario
comment does not cost anything